NEW INFO:See below
READ my new advice
If you are seriously going to study Japanese I STRONGLY STRONGLY urge you to get a Japanese Windows CE palm−size pc. Note: This is not a PALM computer like the Palm Pilot or the Handspring Visor or Sony CLIE. This is a Microsoft Windows CE palm−size PC or Pocket PC made by companies like Casio, HP, Toshiba, Compaq etc...
I'm not partial to Windows CE. In fact for the purpose of a PDA (personal digital assistant) the palm has it's strengths. But, for the purpose of studying Japanese the Japanese Window CE machine wins hands down. Why? Because Japanese Windows CE machines have Handwritten Kanji Recognition Built In!!!! Kanji is the single hardest part of Japanese to learn and without a computer that recognizes Kanji it will take you 2 or 3 minutes PER Kanji too look them up. Imagine trying to read a simple paragraph in Japanese where every word you look up takes 2 or 3 minutes.
Note: I must make a distinction here. If you are going to do this you must get a **JAPANESE** Windows CE machine. You can only buy those in Japan or from a special importer. If you buy an American or European Windows CE machine you will NOT get the Kanji recognition.
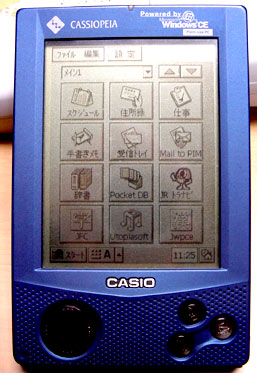
This is the one I got. It is the Cassiopeia E−65. It is not the coolest one on the block. It's black and white. It only has 16meg of memory and it connects either though a serial port or IRdA (infrared port). There is no USB for this model. The advantage is that the batteries last about 12 hours. 12 hours translates into a week or 2 of use without needing new batteries. Of course you can get rechargeable batteries for it which might make the color models more appealing.
This is also the cheapest model and it's about $350.00 not including the cradle and battery which is another $70. For you students I can hear your jaw dropping now and you've already decided it's too expensive but consider this. One, you will NOT be able to really study Japanese unless you are either (a) willing to lookup kanji one at a time 2 to 3 minutes per. I don't know about you but that's a serious deterrent to studying in my book. Of course you don't NEED to know Kanji to start studying Japanese but you will not be able to read one single real world Japanese item, sign, ad, direction etc until you can read Kanji. 🍺 If you look at it as a necessity you can easily consider it not as an *extra* expensive but as part of the cost of learning. Just like you were willing to shell out $120 for your books for example because they were required. Are you then willing to hobble your ability to learn because you can't learn the Kanji? As a side note there is also free Kanji flashcard software for these machines.
There are lots of other models from Casio and HP and soon from Mitsubishi and maybe Compaq. (as of this writing Compaq has not released there i−Paq here in Japan). All of them will work.
One other consideration is that since you are buying a Japanese CE machine you will get ZERO support unless you live in Japan and speak Japanese so if anything goes wrong you are SOL.
All the Japanese CE Machines come with a Japanese <−> English dictionary built in. These have one big problem for learners of Japanese. They are written for Japanese speaking people. That means explanations are in Japanese so although you can look up a Japanese word and see an English equivalent if you look up an English word you will get a Kanji word back with an explanation in Japanese. In other words, something you can't read.
Therefore, once you get it you need to install a Japanese <−> English dictionary for English speaking people. Fortunately such software not only exists, it's FREE!!! You can download it here. It's called JWPCE (for Japanese Word Processor CE) It's actually meant to be a word processor but it has a dictionary built in. I'll try to walk you through installing it since you are on a Japanese machine you will not be able to read the menus to get it started. Note: there is a version for a regular PC too which I find invaluable for corresponding with my Japanese friends.
One of the cool things about this particular dictionary software is that it supports multiple dictionaries. There's the basic dictionary which covers most words. Then there are extra dictionaries for example the medical terms dictionary or the computer terms dictionary. Arguably one of the most useful is the Places and Names dictionary. It's very hard to learn a new language and not be able to tell what is a place or what is a name and how to pronounce them. The only problem with the E−65 machine I own is that it's only got 16meg. After the main dictionary is installed there is only like 6meg left and unfortunately the Places and Names dictionary takes just over 8meg. There are a couple of solutions. Once, get a bigger CE machine that has more memory. Two, add a CompactFlash card. A 16meg card should do. I expect you could get one used for under $40.
The disadvantage to using the Places and Names dictionary is that there are so many names that nearly anything you put in will have a match and your searches will take longer. Fortunately there is an option specifically to exclude the names from your searches.
Installing JWPCE
So, what follows is hopefully an understandable explanation of how to install and use JWPCE.
First you need to download ActiveSync from Microsoft. Generally you can find the latest version at www.pocketpc.com. Just follow the links for downloads until you find ActiveSync. You're in luck because the version you download will be in English. ActiveSync is the software that allows you to upload and download stuff to your CE machine though your PC.
Download it, follow the instructions for installing and running it. Once installed and running you should have your CE machine connected to your PC and there should be an ActiveSync window. In the toolbar for that Window there should be an Explore button. Click it and a folder Window will popup and show you the contents of your CE machine. Browse to the "Program Files" folder and make a new folder called "JWPCE" inside and copy all the correct files for your version of JWPCE (see the instructions for JWPCE).
So far you didn't need me to get this far. The problem is that after you've copied the files you are told to run JWPCE but as you have a Japanese CE machine it's not clear how to do that. Here's how I did it.

figure 1
When I press the *rocket* button (the button with a rocket stamped on it) on my CE machine I get this menu. Each of these icons starts a particular program. What we are going to do is change one icon to be JWPCE.

figure 2
The first thing to do is from the menus pick the first item. This puts you in *edit* mode instead of *use* mode.
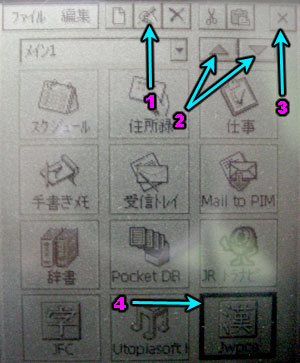
figure 3
Next select the icon you want to change (4). Then click on the edit icon (1). Icons are 12 to a page. If you want to put the icon on a different page use the arrows (2) to switch pages. I'd suggest though that you put it on the first page.
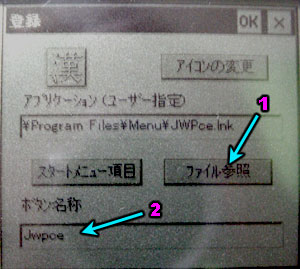
figure 4
Once you've clicked the edit icon you'll get this dialog. Click button (1) and then use the file browser to find JWPCE. This works similar to regular Windows. The drop down list at the top shows folders at the current level. The button to the right of that goes up a folder. Most likely you will need to click once on the *up folder* icon. Then drop down the top list and pick "Program Files", Then drop down the top list again and pick "JWPCE", then drop down the second list and change it to "*.EXE" instead of "*.LNK" and finally select JWPCE.EXE and click "OK" in the top right.
If you want you can enter a name by clicking in the (2) area and then entering a name but as you don't know how to enter text yet I'd learn that first then come back here later. Click "OK" in this dialog then click the "X" close box in the top right (see figure 3 #3)
This will bring you back to *use* mode.
Running JWPCE
If everything went well you should now see an icon for JWPCE in your table of icons. Click on it to start JWPCE. If this is the first time you've run JWPCE it will ask you if it's okay to install it. Pick "Yes" or "Ok".
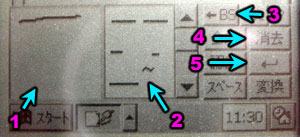
A few things to note: at the bottom of JWPCE you'll see a status bar that looks like this. Where it says "KANJI" (1) that tells you what input mode JWPCE is in. This can be confusing. JWPCE was written for systems that do NOT already have Japanese input methods. The machine you are using DOES have Japanese input methods. Basically in order to be able to enter English you need this to say "ASCII". Click on it to change it. Each time you click on it it will cycle though "KANJI", "ASCII" and "J-ASCII" I have no idea what J-ASCII is. Just make sure it says ASCII
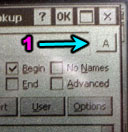
figure 6
If you are in the dictionary dialog you can click this button (1). It will say "K" for Kanji, "A" for ASCII and "J" for J-ASCII. Make sure it says "A".

figure 7
Down at the bottom of the display is the task bar. Actually I'm not sure what Window CE calls it as it doesn't show tasks like regular windows but in the task bar there is a button that looks something like you see here (1 and 2). Clicking on (1) turns on and off input mode. If it's on the bottom 1/4 of the screen will have some way of entering text. If it's off then the whole screen can be used for the current running application. Remember this because sometimes you'll try to display something and it will be covered up by the input area. If get rid of the input area click (1). To bring it back click it again.
Clicking on (2) lets you pick one of the 4 modes of text input. They are as follows
(3) Hiragana / Katakana mode
(4) Romanji mode (Roman characters like we use in English)
(5) Handwriting Lookup
(6) Handwriting Input
I'll try to explain the various modes. The following example generally assume you are using the dictionary so from the menus pick "Util/Dictionary...".
Hiragana / Katakana mode:
This mode shows all 46 hiragana (or katakana) plus the various accents and useful marks like period, comma etc. I never use this mode. I used to think that maybe it would be good to get used to reading hiragana but I find that basically it just slows down my studying. I'm already reading hiragana and katakana in my textbook, homework and reading in general. When I use the dictionary I just want to get back to reading what I was reading as quickly as possible.
---Romaji mode:
This mode shows the alphabet and numbers. This is the mode you would use if you are going to look up an English word or if you already know how to spell / pronounce the word you are looking for
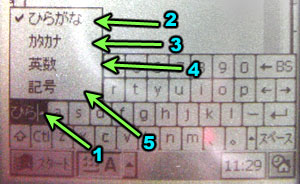
figure 8
|
|
|
|

figure 9
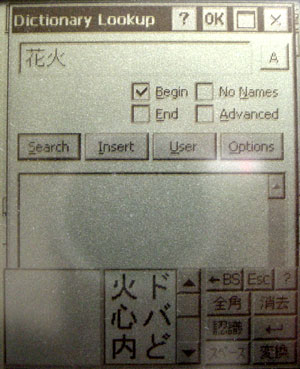
Here is how to use the hiragana submode. Just click on the letters as though it was romanji. For example lets put in "hanabi".

figure 10
I put in the H. Notice that a small window pops up above the input area. This will happen in all modes except English submode. This is to give you a chance to convert your input to kanji before you pass it on to the current program.

figure 11
Next I put in the A. You can see here that as soon as I put in the A it got converted to the character for "ha"

figure 12
Put in N

figure 13
Put in A and I get the character for "na".

figure 14
put in B

figure 15
Put in I and I get the character for "bi".
At this point I could click on the enter button and "hanabi" in hiragana would be entered into JWPCE at which point I could click search (or pick enter again) assuming I'm in the dictionary and it would look up the word. This is usually what you want to do when you are in this mode but there is one other feature.
figure 16
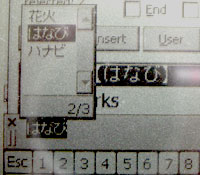
figure 17
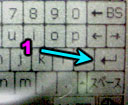
Handwriting Lookup:
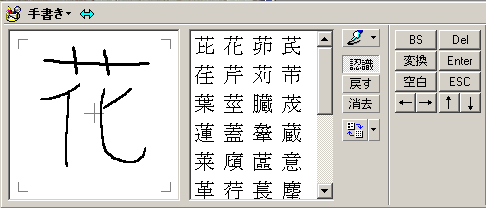
This mode allows you to actually sketch kanji into the CE machine. You can then select from a list of possible matches. So for example you see some kanji on a Japanese magazine and you want to know what it is you can enter it.
Let's enter the kanji for Hanabi (fireworks). I enter the first stroke in area (1). You can see that it's already given me a list of possible matches in area (2). If I click backspace (3) it will erase one stroke at a time until all the stokes are gone, then it will start erasing previously entered characters. (4) is the cancel/reset button. Click it to start over. This will not erase previous characters, just the current one. (5) is the enter button for when you are finished.

Second stroke entered

Third

Forth

Fifth

Sixth

Last one entered. You can see that the Kanji for "Hana" is the first choice in the match area.

To pick it click on it.

You can see that that kanji as appeared in the editing area.

Here I've already entered the Kanji for "bi" and I'm selecting it.

I click enter to put it into JWPCE.
It's been entered. Now I can either click enter again or click on search
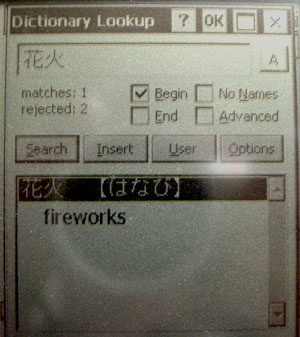
You can see that after entering the Kanji I get the pronunciation in hiragana and the English word "fireworks."
Handwriting Input:
This is the mode that probably most Japanese people would use. It's for people that already know how to write kanji. The difference between it and Handwriting Lookup mode is that this one doesn't give you a list to select from. Basically it just always picks the first one in the list therefore it's important that you draw them correctly.

In this mode you can draw in both squares. The point is that as soon as you start writing in the *next* square it knows that you are finished with the previous square and will immediately pick the best match and put it into the edit area. Here you can see that I've already entered "hana" and I'm in the process of writing "hi" If I had a third kanji to enter I'd switch back to the left as soon as I finished this kanji.
One thing to note, if you pause for more than a couple of seconds it will assume you are finished and pick the best selection so far. If you do not want it to pick (say because you are looking at your magazine trying to figure out how to draw the rest of the character) do NOT remove the stylus from the display. As long as the stylus is still touching the display it will wait for you.
In this mode there is no correcting mistakes. If you pick backspace it will first chose the closest match then immediately erase it so if you mess up just hit backspace and then enter the same character again from the beginning.
Radical Lookup:
This is not part of CE but part of JWPCE itself.
JWPCE has like 9 ways to enter Japanese. I only ever used two. The normal one which I explained above and the following, Radical Lookup. There are two ways to get into Radical Lookup mode. One, if you are in the word processor window you can choose it from the "Kan" menu. If you are in the dictionary, click in the area where you enter a word and then tap your "action" button. On the E−65 the action button is the dial on the left side of the machine. Press it into the machine and click it and a popup menu will appear. You can then use the up and down on the same dial to chose "Radical Lookup" or you use your stylus.
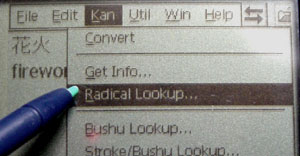
Radicals can be described as the different parts that make up the kanji. For example the kanji for "hanabi" is made up of 3 parts.

The radicals are listed by number of strokes. The top part of "hanabi" is 3 strokes so I look in the 3 area and find that radical and click on it. If you make a mistake just click on it again to unselect it. As soon as I selected it all the kanji that use that radical appear in the list at the top. There are 405 kanji that use that radical. Ugh! So, lets add another radical.

The next one is only 2 strokes. As soon as I select it all the kanji that use BOTH selected radicals show up. This time there are only 16 radicals. I can see "hanabi" is the first one so I could select it and then click "Insert" to insert it into the word processor or dictionary. Note: not every part of every kanji is considered a "radical" as far as I know so sometimes you may not be able to find a particular part in here. Pick another part if that's the case.
Lists and Kanji Info
Sometimes I like to keep lists of words I've looked up. For example if I'm reading a book I might want to keep a list of all the words I've looked up so far either so I can look at the list later for practice or so I can look up a word again quicker than looking it up in the dictionary. For this purpose after you have looked up a word in the dictionary if you select some lines in the dictionary and click "insert" they will get inserted into the word processor.
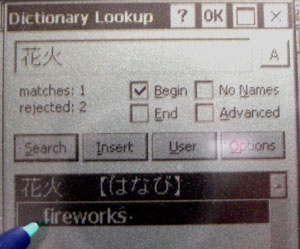
Here I've selected the two lines for "hanabi" then I click insert.
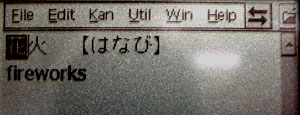
After closing the dictionary you can see that those two lines have been entered into the word processor. One problem though is that JWPCE does not insert a "return" at the end of the last line. That means that the second time you insert something it will insert following the "s" in "fireworks" and not on the line below it. Of course you can go though and edit the file and insert your own returns. More about this below.
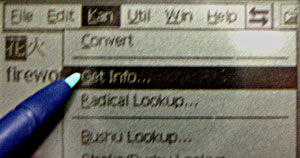
Another thing you can do once you have kanji in the word processor (not the dictionary) is you can get kanji info. Select the kanji you want info on then pick "Get Info...". If no kanji is selected then the first character following the cursor will be looked up.
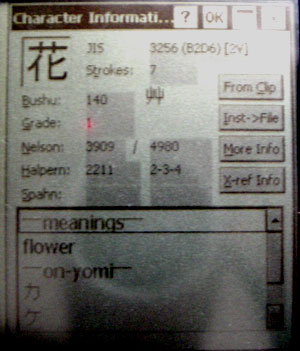
Here is the info for "hana". You can see in the list at the bottom are the basic meanings of that kanji along with the various readings.
Options:
If you pick "Options" from the "Util" menu there is one thing you should probably set. An American CE machine has no Japanese fonts installed but a Japanese CE machine does of course. The advantage to using one of the built in fonts is that they are true type fonts so that can be scaled to any size.
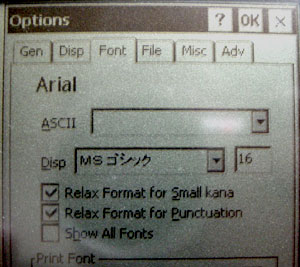
Here you can see that I've set the font to the Japanese version of "MS Gothic" and set the size to 16. 16 is a good size for general usage. There have been a few times I've set it to size 12. The problem with it being small is that you can't read the kanji. The advantage is you can see alot more text.
The other advantage to choosing a built in font here instead of the standard font that is included with JWPCE is that when you pick Kanji info you get a nice clear large character instead of a bitmap scaled blocky character.
Ki o tsukete: Things to be aware of
When you are entering Kanji there are a few things you need to be aware of.
- Stroke Order
Probably the most important is stroke order. Kanji characters are written with each stroke coming in a certain order. If you get the order wrong, odds are high that Windows CE will not find the character you meant to enter. This is very hard for a beginning Kanji learner. There are some basic rules but there are lots of exceptions. This is the #1 reason I sometimes have to use radical lookup mode because if I can't figure out the stroke order then I can't look up the character.
What's worse is that handwritten kanji is often different from printed kanji so printed kanji may appear to have one or two more strokes then you actually need. You'll just have to learn it. Ask your teach for help and gambate! (Hang in there)
- Number of Strokes
The number of strokes is also very important. If you get it wrong then your stroke order will be off also
![]()
For example this character is 3 strokes, not 1 and not 2
![]()
and this character is 2 strokes not 3.
- Stroke direction
Even stroke direction is important. Usually all strokes are left to right and top to bottom but not always.
- Staying inside the box
Another thing to be careful off is that you must draw inside the box (The area where you draw kanji). If you make a mistake and draw outside the box, especially off the top, that click off the top of the box translates into a click into your application. This means for example that if you are in the dictionary, all of a sudden you are no longer entering text into the area where you lookup words but instead you have made the dictionary's result list area active and are therefore trying to enter text into that list. Of course you can't enter text into that list so as you try to type more characters they don't appear anywhere. Click in the dictionary input area again to fix that.
- Slow using Handwriting lookup mode
When you use handwriting lookup mode as you enter each stroke the matches come up nice and quick but when you finally select a character from the list of matches it can take up to 5 seconds for it to appear in the edit area. Why this is only the programmer of that part of the OS knows. It's clearly poorly designed. I think the reason it hasn't been fixed is that Japanese people probably don't use that mode, only students and there aren't many of those so it's a very low priority. If the guy that wrote that part of the OS actually used that feature he'd be so frustrated he'd fix it immediately. Try it. Type your name on your computer now but after each letter say "one one thousand, two one thousand, three one thousand, four one thousand, five one thousand" before you can type the next letter.
I checked to see if this had been fixed in new versions of Windows CE but it has not. Of course the faster processors on the newer machines have helped. They only take 3 seconds but still it's frustrating. Try the above example again but only count to "three one thousand" and it's still painful. I wish I knew how to get a hold of the guy that's responsible for that so he could fix it. I'll bet he not even aware of the problem.
- Input focus
Be aware of where the input focus is. The input focus is the place where input is going to go when you enter letters. For example when you are in the dictionary it could be 1 of 3 places. It could be in the place where you enter words you want to lookup. This is the place you want it to be. It could be in the list of results. You generally don't want it there. It could also be in the word processor window behind the dictionary window. This is very confusing. To make it be in the lookup word place click there.
- Knowing where words start and stop
Unlike most Western languages there are no spaces between words in Japanese. That mean that knowing where one word starts and one ends is difficult for students. A couple of hints. Generally, kanji marks the start of a word and generally kanji words are 1 or 2 kanjis long. There are lots of exceptions but if you see 4 kanjis in a row, more often than not that's two 2 kanji words. If you see three kanji and you enter all 3 in the dictionary and you don't get a match. Try looking up just the first 2. If that doesn't work try just the last 2.
- Having *insert* insert a return
This is not a "be" careful thing but more of a hope. It would be nice if there was an option you could set that would make JWPCE insert a "return" at the end of a selection in the dictionary when you insert it into the word processor. This would not only be useful for lists but it would also be useful for making vocabulary lists for JFC, the flashcard program by the same person as JWPCE. As it is you have to hand edit those lists. If this open was added you could make the flashcard lists alot faster.
- CE lockups
Windows CE arguably has some design flaws or maybe they should be called trade offs. Basically, Window CE uses a system of memory management that basically means that you can put more on the machine than you can run at once. This is the same as a regular PC. You can't run 50 applications with only 16 meg of memory. Unfortunately Windows CE will let you try and when you fill up the memory it will basically lockup. That's what the reset button is for on the back of the machine. A Palm Pilot / Visor solves this problem by not letting you put more programs in it than you can run all together. In fact, on a palm, all your installed applications are ALWAYS running. That means switching from one to another is instant. It also means no lockups. On the other hand it means you can't install as many applications as CE or as big applications.
Windows 2000's IME
All versions of Japanese Windows include a Japanese IME (Input Method Editor) This is what lets Japanese people enter Japanese. That's cool for them but what about a non Japanese speaking person running non Japanese windows.
Well, Microsoft gives away for free that they called "Active IME". This is the one that you can download from the Windows Update / Internet Explorer website. That's cool and it lets you enter Japanese but it doesn't let you enter handwritten Kanji.
Well, what some of you may not know is that for all versions of Windows except for Windows 2000 the Japanese and American versions of Windows are separate and different programs BUT, for Windows 2000, the two versions are actually the very same software with just different settings as the default. What does this mean? It means if you are running English Windows 2000 you can turn on the REAL Japanese Input Method editor and then you can enter handwritten Kanji on your PC without having to install a Japanese OS.
You turn it on by double−clicking on the "Regional Options" control panel. Then under the "General" tab in the "Language Settings for this System" you need to set the checkmark for Japanese. You may need to click "Advanced..." and add Japanese first and then reboot once for it to appear. After that you can go to the "Input Locales" tab and add the "Japanese Input System (MS−IME2000)". Once you do, next time you reboot you'll see in the tool tray an Icon that says "EN". Click it and select the other icon to be in Japanese mode (or you can set Japanese mode to be the default in the control panel.)
When in Japanese mode here are a few shortcuts. By default you are still typing English. To switch to Japanese input press "Alt Tilda". To switch back press it again. Of course you can pick it from the IME Window. It's the first icon.
If you are in Japanese mode and you want to type some English in the middle of some Japanese here's what you do. Just type the English (no spaces allowed as space starts conversion into Kanji). Once you have the word entered and it's all gobbley Japanese, press F9 to convert to romanji then press F8 to convert it to ASCII.
To enter an ASCII space instead of a Japanese space press "Shift−Space".
If the IME Window is getting in your way right click it and pick the top item from the menu. This will insert it into the tool tray.
Right clicking on either the IME Window or it's icon in the tool tray and picking the icon that looks like a bucket with a pencil in it will bring up the handwriting input mode as seen here. The biggest advantage to this one over the CE one is that it's more forgiving about stroke order (though not that much). The disadvantage is that unless you have a graphic tablet or a touch screen it's slower to draw the kanji with a mouse instead of a pen.
If you get a different window, click just to the right of the icon in the top left of the window and from the menu select the item that looks like the one in the picture above that's just right of the icon.
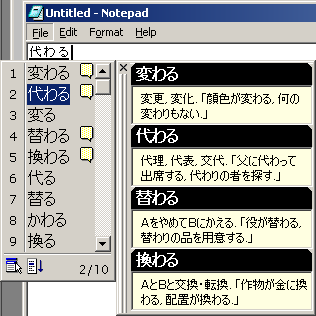
Another cool thing about the Windows 2000 IME is that when you press space to convert your hiragana to kanji, after you've pressed space a couple of times and the IME pops up the list with all possible matches it will sometimes pop up a list showing you the meanings of the different kanji. Of course it's in Japanese since it's meant for Japanese speaking people but after you've been a student for a while you can often figure out which is the kanji you want from the parts of the explanations you recognize.
About the conversion from hiragana into kanji. The IME does not show all possible conversions. I don't know why this is. I suspect it's because all possible conversions are not known since Japanese is so complicated and is constantly changing. I know it doesn't show all possible combinations because one of my friends wanted to enter her name and she knew it wasn't in there. But, she also knew how to configure it so it was. Of course all the info is all in Japanese dialog boxes so I haven't a clue how to do it but if you want to dig around it is there.
Wishes
The following are some of the things I wish this combination of hardware and software would do. I'm willing to help out. I'm not complaining. These are just suggestions for improvements that would help me tremendously as a student of Japanese.
- Japanese coded English
I mentioned this above but JWPCE's dictionary does not like romanji coded outside of the ASCII character set. It would be simple matter to fix this and would not effect any of the functions. Maybe I'll look into fixing that myself.
- Antonyms, Synonyms
This is more an issue of the dictionary which is actually separate from the JWPCE software. Basically it would be way cool if you could look up antonyms and synonyms. I know there is work in that direction so maybe it will happen someday.
- Usage / Examples
This would make the dictionary very large but it would be really useful to have usage examples. This is not a real example but for example if you look up "fly" you get "hae" and "tobu". Which one means fly as in the the bug and which one means fly is in "birds fly". There's often no way of knowing.
- and, or, not, regular expressions
The dictionary search in JWPCE is alot better than the built in Japanese CE dictionary because all the built in one does emulate a real dictionary. That means if you look up "kei" it will just basically turn you to the page in the dictionary that has the first word that starts with "kei" where as the JWPCE dictionary will return all words that have "kei" anywhere in them. You can choose "begin" if you want only words that start with "kei" or you can choose "end" of you only want works that end with "kei" or you can choose both "begin" and "end" if you only want the word "kei".
But, it would still be cool of you could use things like and/or/not and or regular expressions. This would allow you to search for all words that started with "t" and ended in "kei" for example. That would make it much easier to look up words that you heard but didn't hear well enough to spell perfectly. (I've been told that this is in the works)
- "to jump"
Also currently, if you look up "jump" you'll get 57 matches. If you look up "to jump" you'll get zero matches even though all the verbs for jump are listed with "to jump". It would be nice if that was fixed because I often want to lookup just the verbs (This is fixed as of version 1.4 of JWPCE)
- verbs, adjectives, nouns,...
This again is related to the dictionary more than JWPCE. It would be cool though if the information was there that you could search and select type of word you want. For example I want the word "jump" and I want a noun as in "the thing that Evil Kenevil" uses in his stunts.
Corresponding with Japanese friends
This is separate from CE and more specific to JWPCE on my PC. I use it daily to read and write e−mail with my Japanese friends. I works like this. First, I use MS Outlook so I'm sure about other software but I know you can write Japanese with Outlook Express also if you download the Japanese Input from Microsoft or if you are running Windows 2000.
I receive a message. I copy and paste in into JWPCE where I can select words and hit F6 to pop the dictionary for words I don't know.
Then I type replies into Outlook (or Outlook express) and when I don't know a word or I don't know which kanji to select from the list of kanji I pop over to JWPCE and quickly use the dictionary for help.
I was told that there is some work going on in integrating the dictionary into Outlook / Outlook express but I'm not sure how that progress is going.
One other caveat: If you use the Active IME (the one you download from Microsoft) you can only write Japanese e−mail in HTML. The reason is is that the Active IME plugs into the HTML editor so if you aren't editing HTML then you can't use the Active IME. This can be a problem because your friends in Japan may not have an e−mail program that reads HTML e−mail. Surprising but actually I found that more than 50% of my friends could not read my e−mail if it was in HTML. Especially if they are reading it at work.
That's another good reason to run Windows 2000. Since it has Japanese support built in you can type Japanese anywhere. Not just in HTML places. So, you can then send plain text messages with Japanese in them. Note: When you make a new message you need to pick "Format/Encoding/Japanese" before you send the message or Outlook will complain that you have non English characters in your message.
Another note: In order to be able to cut and paste FROM JWPCE to another program in Windows you generally need to set the options in JWPCE under the "clipboard" tab where is says "Export" to "UNICODE"
New Dictionary Software
2002/05/03
You can probably see from some of the discussion below that there are a few things I've run into with my CE machine. Specifically the EDICT dictionary that JWPCE uses is not the greatest dictionary. It works, it's functional but it has no example sentences and if you are searching English to Japanese you often get too many hits because the actually dictionary is Japanese to English meaning the dictionary has one Japanese word followed by it's definition. When searching for English words it just gives you every definition with that contains the word you searched for.
So if you search for "jump" you might get
tobu: to jump
but you might also get
mizutamari: puddle, jump in the puddle
because the word "jump" is in the definition of "mizutamari". (note: I made that example up)
Some people recommend some of the other electronic dictionaries. A particular bargin is the Canon Wordtank IDF−3000 which has English menus and an English manual. The advantage is it has a much better dictionary with examples and it has both English to Japanese and Japanese to English dictionaries. The disadvantages are, both dictionaries are meant for Japanese speaking people so there will be lots of words in Kanji etc which makes it of limited use. The other #1 disadvantage is there is no good kanji input.
But, as my Japanese is now at a pretty good level so that I can generally kind of work through the Japanese definitions I had been thinking about getting an IDF−3000. They are only about 12000 yen.&nbs p; About $100 U.S. The problem is of course then I would end up carrying two machines all the time. My CE machine to lookup kanji and the wordtank to lookup works when I know the pronunciation. I just couldn't get myself to do it though because I knew I would pretty much never pull out the wordtank. I would try to look stuff up first in the CE machine and then only if the definition was not clear enough and if I was not too busy/lazy I'd finally get out the wordtank.
Well, I found out a company makes some good dictionaries for CE machines. Specifically a company called Logovista is selling about 6 different dictionaries for CE machines.
I picked up two of them. The Leaders English to Japanese dictionary version 2 with about 270,000 entries and the Japanese Koujien Dictionary version 5 with 230,000 entries.
The Koujien dictionary is for Japanese people to lookup Japanese words. As such there is little to no English in it. But, at some point in your later studies you should probably start using a Japanese dictionary.
They are both about 10800 yen each, about $85 U.S. That may sound like alot of money but if you were to buy them in book form they are each about 3000 pages and cost 7800 yen each. Here's the Leaders in book form and the Koujien in book form. I have not seen the Leader book in the flesh but the Koujien book is like 3 inches thick so I'm happy to pay an extra 3000 yen in order to carry it in my CE machine instead of the actual book.
On top of that you will need at least a 128meg memory card for your CE machine. The Leaders dictionary takes 52meg and the Koujien takes 38meg.
That would bring the total cost of the cheapest CE system with those two dictionaries to about 60000 yen. About $520. For me it's worth it. I can use similar dictionaries to the Wordtank if not in some ways better ones and I have kanji input as well as other functions plus I still have access to JWPCE and EDICT dictionary and the JFC flashcard software.
But, so far there is at least one drawback. The Leaders dictionary is English to Japanese not Japanese to English. You enter an English word and it will give you a list of matching or close to matching. Here is one entry for "develop"
de・vel・op, -ope /d#v#l#p/ #vt
1a 発達[発育]させる, 発展させる〈from, into〉; 【生】 発生させる, 進化させる.
b <議論・思索などを〉展開する (evolve), 詳しく説く; 【数・楽】 展開する.
2 <新しいものを〉創り出す; 〈資源・土地を〉開発する, 〈宅地を〉造成する, 〈鉱山などを〉開く.
3a <潜在力・傾向などを〉発現[顕出]させる, 発揮する; #〈新事実などを〉明らかにする; 【写】 現像する.
・develop cancer 癌になる.
・He developed fever. 熱を出した.
・print the developed films 現像したフィルムを焼き付ける.
・developed colors 顕色染料.
・a developing tray [tank] 現像皿[タンク].
b <事故・火災などを〉起こす.
4 【軍】 〈攻撃を〉開始する, 展開する; 【チェス】 〈コマを〉動かす. #vi
1a 発育[発達]する (grow) 〈from, into〉; 【生】 発生する, 進化する; 発展する〈into〉; 進展する.
・A blossom develops from a bud. 花はつぼみから発育する.
・A bud develops into a blossom. つぼみは発育して花となる.
・Gossip develops into fact. うわさが長じて事実となる.
b (新たに)生ずる; 〈病気が〉発現する; 【写】 現像される; #明らかになる, 知れる.
・Symptoms of cancer developed. 癌の症状が現われた.
・It developed that ということが明らかになった.
2 【チェス】 コマを動かす. de・v#l・op・able a 発達[発展]させられる; 展開可能の.
[F (veloper to wrap)<Romanic<?; cf. ENVELOP][株式会社研究社 リーダーズ英和辞典第2版]
(note: the #s above are characters that didn't not covert when I pasted it here)
That's great. But, it's an English to Japanese dictionary NOT a Japanese to English dictionary. If I enter Japanese, first, it will only lookup words as they are in the dictionary meaning you can enter 開発 but not かいはつ so if you don't already know the kanji it would be hard to use that way. Second, because it's English is does not give you the definition of 開発 but instead it looks up the English word that's closest too 開発 which is develop and then shows you the definition for "develop" like above.
The solution is to either lookup Japanese words in the Koujien dictionary and try to understand the definition in Japanese OR to get a Japanese to English dictionary. The company above sells one. The Daily Concise English-Japanese AND Japanese-English dictionary. I can't tell you how good it is though because I have not purchased it....yet 😊. Given that's both English−>Japanese and Japanese−>English I probably don't really need the Leaders dictionary above, and for most students they probably don't need the Koujien dictionary either. But, this dictionary has only 70000 Japanese−>English entries and about 77000 English−>Japanese entries. It takes about 17meg on the memory card at it's 6800yen. About $50. The book version is 2920yen. About $25 U.S.
I have a feeling these products have not sold well. The cross over from the number of Japanese people that (1) have a CE machine and (2) need one of these dictionaries is probably pretty small. Plus, my CE machine already has a built in Japanese dictionary, Japanese->English Dictionary and English->Japanese dictionary. It's has respectively, 50,000 words, 27,000 words and 40,000 words and the kanji dictionary is separate meaning you cannot enter words in Kanji into the Japanese−>English dictionary. But, the point is for Japanese people this is probably enough that they would not consider getting a better one.
As for installing they have made it pretty simple. Copy the setup folder (not just the contents) of the correct version of the software for your machine from the CD to the root folder of your memory card, copy the dictionary folder (not just the contents) from the CD to the root folder of your memory card. On the CE machine run the setup program off the card. It will copy the software to the internal memory of the CE machine and leave the dictionary on the card. You can then delete the setup folder if you want. That's nice. I was pretty worried if I had to copy 100meg worth of stuff over my 9600 baud serial connection it would have taken 29 hours.
New CE Machines
2002/05/03
Every year of course new CE machines come out. Other than money, the biggest turn off for me on these new machines is with fast processors and color displays the batteries last 1/4 the time as my old E−65.
But, while I was writing the previous section I noticed a few things Casio is providing with their latest, the Cassiopiea E-2000. One it's got 64 meg of memory, both Smart Media AND CompactFlash slots including type 2. It's got what looks like it's the same dictionary I have in my E−65. It's got Transland English->Japanese and Japanese->English translation software which might be cool and, like my E−65 it has JR's Travel Navigator. How useful that is if you are just starting Japanese I'm not sure but I use it all the time. You put in a starting train station and an ending train station and it will give you a list of various routes to get there and how much they cost and how long they take.
New Advice: Should you get one?
2002/05/03
I get asked at school all the time about my CE machine and as much as I love it and as much as I feel I could not study without out it etc etc, when other students ask about it I generally tell them the pluses (Kanji lookup, English in EDICT, Flashcards etc) but also the minuses. To me, a minor one is price $300 to $600 is nothing compared to not progressing as fast as you could because you cheaped out on study aids. But, the big issue is...It's complicated to use one of these things. You need to be comfortable using a computer. You'll need a computer too. You need to connect the CE cradle to the computer so you can upload JWPCE, JFC and EDICT. You need to get a compact flash card for the other dictionaries if you want them and be able to figure out how to navigate the menus etc to get the software installed and running. For me that's no problem. My hobby is computers. My job is computers. But for most students it might be a problem so before you run out and get one please consider that.
Of course that's why I wrote this page. So if you do get one you'll at least have some idea of how to get it setup and how to use it. 😉
Using a non Casio Battery
2002/11/03
My E−65 seemed to be running out of juice almost instantly lately. I have a few Nickel Metal Hydride (NiHM) AAA batteries around and it's fine to just use them instead of the battery that came with my Cassiopeia but a minor annoyance not to have it just charge in it's cradle.

the original battery
So, I stuck two NiMH batteries in and stuck it in the cradle and noticed that the charge light did not come on. Looking at the original battery I couldn't see anything obvious like a 3rd contact or anything but then I looked in the battery compartment itself.

the extra contact
There is an extra contact. If you look back at the original battery you can see one side is uncovered making contact with that extra connector in the compartment. So, I stripped the cover off one of my NiMH batteries.

the stripped battery
I dropped it in the cradle and the light came on, charging. So far so good. It seems to be working and I don't have to go hunt down a custom Casio battery that would probably cost 2 to 4 times more than generic NiMH batteries.
Note of course I am not an electrical engineer so I have no idea if it's possible that charging non Casio batteries in here will burn my house down or something similar so if you are going to try this too you do so at your own risk. My rationalization was that if it broke my E-65 then I'd just have an excuse to go out and buy a fancier Pocket PC 😛




